SofGAN学习笔记

SofGAN: A Portrait Image Generator with Dynamic Styling

原文链接

SofGAN: A Portrait Image Generator with Dynamic Styling. ACM Trans. Graph. 41(1): 1:1-1:26 (2022)

近年来，生成对抗网络（Generative adversative Networks, GAN）被广泛用于肖像图生成。然而，在GAN学习到的潜在空间中，不同的属性，例如姿势，形状和纹理风格，通常会相互纠缠，使得对特定属性的显式控制变得困难。为了解决这个问题，我们提出SofGAN图像生成器，把肖像的潜在空间分离成两个子空间：几何空间和纹理空间。从两个子空间中采样的潜在编码被分别送入两个网络分支，一个用于生成具有标准姿势的3D几何图形，另一个用于生成纹理。对齐的3D几何图形还带有语义分割，被编码为语义占用域（semantic occupancy field, SOF）。SOF允许在任意视图中呈现一致的2D语义分割映射，然后将其与生成的纹理映射融合，并使用我们的语义实例（semantic instance-wise, SIW）模块将其风格化（stylized）为肖像图片。通过大量实验，我们证明了我们的系统能生成高质量肖像图，并且具有独立可控的几何和纹理属性。该方法也适用于各种应用，例如外观一致的人脸动画和动态风格。代码可在sofgan.github.io获得。

4 GEOMETRY MODELING

以前的方法使用有符号距离函数（signed distance function, SDF）或占用域（occupancy field, OF）作为3D点或网格的替代几何表示（representation）。例如，SDF函数$\mathcal{F}(x)$定义了$\mathbb{R}^3$模型的有符号距离(signed distance value)或占用概率（occupancy probability）。此类函数仅描述表面几何（空间位置，法线（normal）等）但不考虑表面语义。我们观察到，这些语义成分对真实感图像的生成至关重要：它们为生成令人信服的纹理和着色细节提供了关键指导。

  相反，我们使用一种新的语义占用域（semantic occupancy field, SOF）表示，它通过将输入点$x \in \mathbb{R}^3$映射到$k$-维向量来扩展SDF，以描述其属于$k$种不同的语义类别（例如眼睛，嘴，头发，帽子，衣服等）的占用概率。在SOF中结合语义标签域几何图形有几个关键好处。

（1）由语义类别定义的区域是区域风格合成和调整的基本单位。这种对肖像的各个组成部分（例如头发 vs. 眼睛 vs. 嘴巴）的区域性控制大大优于将图像视为单个实体的蛮力方法。

（2）自由视角图像生成是SOF的自然延伸，可以无缝集成到深度网络中：SOF描述了可以通过后续神经渲染直接合成的新视图的几何属性。

  SOF将几何和语义标签建模为：

其中语义占用函数$\mathcal{F}(x)$给每一个在3D空间中的点$x \in \mathbb{R}^3$分配了一个基于$k$个语义类别的$k$维概率（$P_x$）。

4.1 Neural SOF Representation

受最近的神经场景表示（neural scene representations）启发，我们使用两个多层感知机（MLP）来估计$\mathcal{F}$，一个SOF网络$\Theta$，和一个分类器$\Phi$。如Fig. 4所示，$\Theta$将每个空间位置$x \in \mathbb{R}^3$映射为一个特征向量$f \in \mathbb{R}^n$，它对语义属性进行编码，而$\Phi$对应一个语义分类器，通过softmax激活把$f$解码为$k$维语义概率向量$P_x$：

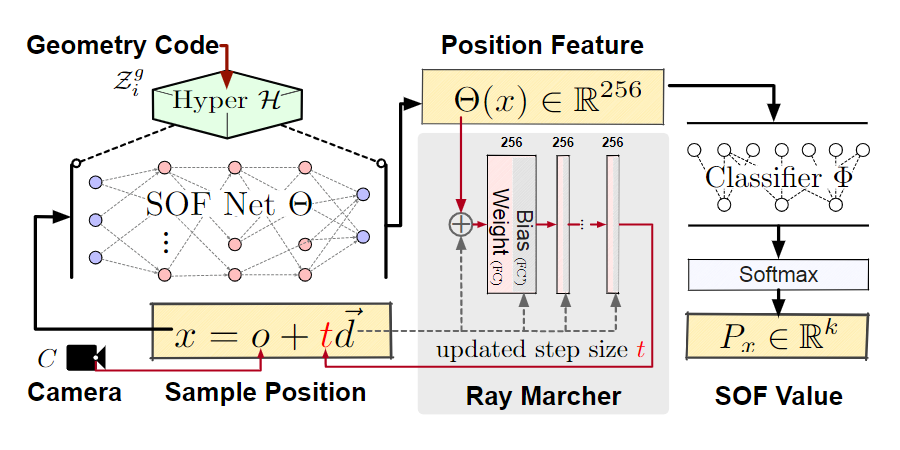
Fig. 4. The free viewpoint segmaps rendering process. Given a query camera C and geometric latent code z_i^g, we first use a hypernet H to compute the weight of SOF network(Θ). Next we conduct ray casting on SOF. To render each pixel, we cast its corresponding ray towards the SOF, starting from the given camera's Center-of-Projection(CoP) o. We conduct iterative depth refinement using the SOF where the refinement step is also computed from an MLP-based ray marcher. Finally we feed the estimated surface point and its feature vector to the classifier Φ to decode them into a k-class semantic probability P_s ∈ R^k.

  我们通过将已知的3D肖像模型渲染成多视角分割图（segmentation maps, segmaps）来训练SOF，并计算渲染的segmaps和实际的segmaps的二元交叉损失。如附录中Fig. 19所示，可以通过对真实多角度肖像图进行语义分析，或通过语义标签（例如，纹理上）渲染合成3D模型来获取实际分割图。

  为了解决3D肖像的多样性，蛮力方法是为每个肖像实例训练一个单独的SOF。这种方法效率很低，因此不适用于实际应用。相反，我们训练了一个几何采样空间，以便使用潜在编码在潜在空间中支持各种肖像实例。我们观察到，3D人像展示了相似的布局，即眼睛，头发，鼻子和嘴唇遵循一致的空间布局。这使我们能够训练一个共享的规范潜在几何空间。具体来说，对于每个实例的网络，我们采用了一个共享的超网络$\mathcal{H}$（Fig. 4）来学习SOF网络$\Theta$的权重。在共享的超网络下，我们可以用一个潜在向量$z^g$表示训练数据集中的每个实例：

其中$i$代表训练集$\mathcal{D}$中的第$i$个实例。我们使用所有的$z^g$来组成具有高斯混合模型的几何采样空间$\mathcal{G}$。在我们的实现中，我们构建了一个由122个分割好的肖像扫描构成的数据集，对于每个模型，我们随机选取视角渲染了64个分割图。

4.2 Free-Viewpoint Segmap Rendering

给定训练好的SOF，我们随后可以渲染自由视角分割图。Fig. 4详细展示了渲染过程：我们通过射线行进策略和估计每条射线的深度$t$（从相机中心到表面）从SOF中提取肖像表面，总共为$N$步行进步长$t_i, i \in [1, N]$。肖像表面$\mathcal{S}$对应于点：

对于每个前向渲染过程，我们首先向场景投射射线，然后使用射线行进策略获取表面点$x$（Fig. 5中间）通过迭代来估计行进步长$t_i$，最后用Eq. 3预测语义性质。射线行进中的步伐递增可以使用LSTM网络模拟，并且实现了令人满意的场景表示性能。然而，我们观察到LSTM架构在视角变化期间非常不稳定并且对新视角很敏感，如附录Fig. 15所示。

Fig. 5. SOF is a 3-dimensional volume, with a k-class semantic probability for each spatial point. The probability for each semantic class also forms a contiguous 3D volume (left). For each position, we take the semantic value with max probability and adopt a differentiable ray marching scheme (middle) to render it into 2D segmentation maps (right).

  因此，我们提出了一种更稳定的射线行进器（Fig. 4中间），它可以根据当前位置特征和射线方向预测步长。每个射线行进MLP层包含两个子全连接层$FC_i$和$FC_i’$，其中$FC_i$是一个没有添加偏置的线性映射（即，$b$在线性层$y = xA^T + b$）同时$FC_i’$将射线方向映射为层偏置。

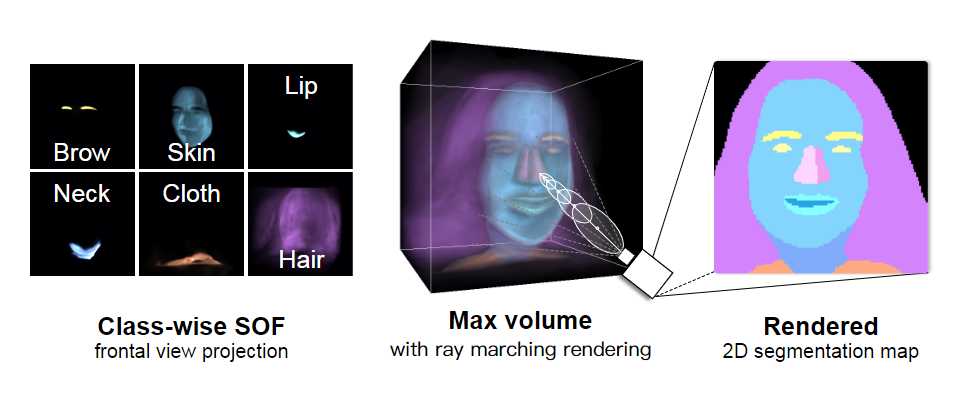
  Fig. 5展示了一个对空间中每个点都预测了语义标签的样本SOF（我们只展示了对应于最高概率的标签）。我们还展示了我们提出的MLP射线行进模块在渲染质量上的改进，该模块优于附录Fig. 15中的LSTM。

为了在推理阶段进一步确保视角之间的深度一致性，我们使用了行进块（marching cube, MC）算法提取了一个粗略的肖像代理（proxy），并使用重新投影的深度作为射线行进的初始深度。