AdaMatting学习笔记

Disentangled Image Matting

原文链接

Disentangled Image Matting. ICCV 2019: 8818-8827

摘要

  大多数以前的抠图方法需要一个粗略的trimap作为输入，然后给每个处于trimap未知区域的像素估计一个分数（fractional）alpha值。在本文中，我们证明了从一个粗略的trimap中直接估计alpha蒙板（alpha matte）是先前方法的主要弊端，因为这种做法试图同时解决两个本质上不同的问题：识别trimap区域内的真混合像素（blending pixels），并为它们估计出准确的alpha值。我们提出了AdaMatting，一个新的端到端抠图框架，它将这个问题分解为两个子任务：trimap自适应（adaption）和alpha估计。Trimap自适应是一个像素级分类问题，它通过识别明确的前景（foreground）、背景（background）和半透明（semi-transparent）图像区域来推断输入图像的全局结构。Alpha估计是一个回归问题，用于计算每个混合像素的不透明度。我们的方法在一个深度卷积神经网络（CNN）中分别处理这两个子任务。大量实验表明，AdaMatting具有额外的结构感知能力和trimap容错能力。我们的方法在Adobe Composition-1k数据集上实现了最先进的定性和定量性能。它也是目前alphamatting.com在线评估所有常用指标中表现最好的方法。

1. 介绍

  图像抠图是指在图像和视频序列中准确估计前景对象不透明度的问题。…。形式上，输入图像$I$被建模为前景色和背景色的线性组合，如下所示：

$$I_i = \alpha_iF_i + (1 - \alpha_i)B_i, \alpha_i \in [0, 1], \tag{1}$$

  其中$F_i$、$B_i$和$\alpha_i$分别表示像素$i$处的前景色、背景色和$\alpha$蒙板估计。给定输入图像$I$，图像抠图的目标是同时求解$F$、$B$和$\alpha$。该问题是高度不适定的（ill-posed），根据Eq. 1，对于一张RGB图像，需要求解7个值，但每个像素只有3个值已知。大多数现有的抠图算法，约束解空间的必要输入是trimap，这是一种表示不透明区域和未知区域的粗略分割。Trimap可以由用户涂鸦生成，也可以由二值图像分割自动生成。无论那种情况，输入的trimap都比较粗糙，…。这是因为通过手动标记提供准确的trimap是很枯燥的，而且现有的图像分割方法很难在低分辨率图像上运行。

  不幸的是，以前的图像抠图方法经常忽略了输入trimap的不精确性，并试图从中估计出一个好的alpha蒙板。我们认为，在这个过程中，有一个分类问题没有得到充分解决。如果我们仔细观察trimap，未知区域中的像素可被归类为三种：不透明前景、不透明背景和半透明区域。我们称前两种类型为不透明像素（opaque pixels），最后一种类型为混合像素（blended pixels）。图像抠图的理想行为是为不透明像素生成精确的0或1，同时精确估计混合像素的不透明度分数（介于0和1之间）。从这个角度来看，两个相关但本质上不同的任务隐含在图像抠图中。第一个是区分未知区域中的像素是否为混合像素，我们称之为trimap自适应。第二个是精确计算混合像素的不透明度分数，我们称之为alpha估计。

3. 方法

3.1. Trimap自适应

  我们首先正式定义trimap自适应的任务。定义$\alpha_{gt}$为alpha蒙板ground truth。相应的图像最佳trimap $T_{opt}$可被自然地定义为：

$$T_{opt}(x, y) = \begin{cases} background\ \ \ \ if\ \alpha_{gt}(x, y) = 0,\\ unknown\ \ \ \ \ \ \ \ if\ 0\lt\alpha_{gt}(x, y)\lt1,\\ foreground\ \ \ \ if\ \alpha_{gt}(x, y) = 1, \end{cases} \tag{2}$$

其中$(x, y)$代表每个像素在图像中的位置。给定一个带有trimap的图像（可能是是粗略的），trimap自适应旨在预测最佳的trimap $T_{opt}$。直觉上，在trimap自适应中，我们将半透明区域从不透明前景和背景中分离开来。这让人想起语义分割任务（semantic segmentation task），该任务也可将图像划分为离散的部分。根据上面定义的$T_{opt}$，图像抠图任务自然地分成了两个步骤：(1) 确定alpha为零、一或者都不是，(2) 如果区域被认为是半透明的，则计算精确的alpha。注意，我们不要求预测的标签与输入的trimap完全兼容：如果用户输入包含小错误，我们希望我们的模型能够纠正它。

3.2. 网络概述

  如上所述，trimap自适应需要对物体形状和结构有更多的语义理解，而图像抠图则更多依赖于谨慎地利用光度信息（photometric cues）。同时解决这两个问题，同时共享中间表示（representation），可以提高整个模型的性能。因此我们设计了一个完全端到端的CNN模型，名为AdaMatting。Fig. 2描绘了AdaMatting的流程，它包括一个产生共享表示的编码器，然后是两个相关的（dependent）解码器，分别解决trimap自适应和alpha估计。Trimap自适应的结果和中间alpha蒙板随后被送入传播单元（propagation unit），形成最后的alpha蒙板。

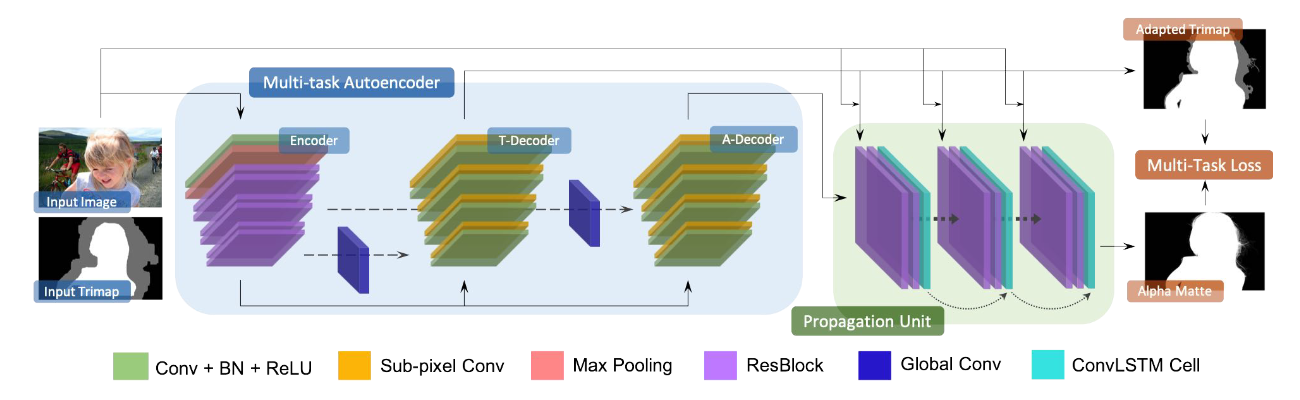Figure 2. Pipeline of the proposed AdaMatting. T-Dcoder and A-Dcoder stand for trimap decoder and alpha decoder, respectively. Symmetric shortcuts are linked to different levels of layer for the two decoders.

  AdaMatting将一张图像和其对应的trimap作为输入。首先，一个前端的全卷积编码器（参考了ResNet-50）产生深度特征（feature）用作共享表示（representation）。然后两个独立的解码器被应用于每个任务，旨在学习从共享表示到所需输出之间的映射。每个解码器由几个3$\times$3卷积层和上采样模块组成。Trimap解码器在交叉熵损失的引导下输出3通道的分类向量（classification logits）。Alpha解码器输出一个1通道的中间alpha估计，该估计被送往传播单元以进一步细化。

  多任务自编码器（Multi-task Autoencoder）我们的流程中的主要模块是基于广泛使用的U-Net架构设计的多任务自编码器，因为它在许多计算机视觉任务中取得了很大的成功。根据trimap自适应更依赖于高级特征并且alpha估计更依赖于低级特征的观察，两个解码器的不同层之间有一些对称的shortcuts。更具体地说，trimap解码器采用了深层和中层的shortcuts，alpha解码器采用了中层和浅层的shortcuts。此外，最近的研究表明，有效感受野的大小在分割任务中起着重要作用。为了进一步扩大感受野的同时保持可接受的计算成本，在shortcuts上采用了全局卷积（global convolutions）。这个改进进一步扩大了感受野，有助于获得更可靠的和局部一致（locally consistent）的结果。

  传播单元（Propagation Unit）受到广泛使用的基于传播的（propagation-based）的方法的启发，我们设计了一个传播单元，该单元由最近的先进成果卷积长短期记忆（LSTM）网络实现。如Fig. 2所示，该单元由两个ResBlocks[17]和一个卷积LSTM单元组成。在每次循环迭代中，将输入图像、调整后的trimap和之前的alpha蒙板传播结果作为输入。ResBlock从输入中提取特征，而卷积LSTM单元在各步传播之间保存记忆。

  与传统的基于传播的方法类似，传播单元逐步细化预测的alpha蒙板，产生具有更准确的边缘细节和显著减少不希望出现的伪影的最终结果。Fig. 3展示了如何在所设计的传播单元内细化alpha蒙板。可以看出，头发逐渐变得更清晰。而且，在传播过程中消除了模糊伪影。

Figure 3. Visualization of the propagation intermediate alpha mattes. Artifacts are gradually removed and the hair progressively becomes clearer and more distinguishable.

3.3. 多任务损失（Multi-task Loss）

  多任务学习的目的是在一个模型中解决多个任务，同时与单独训练的模型相比，实现更高的效率和性能。它可以被认为是一种通过在互补任务中共享域信息（domain information）来促进知识转移（knowledge transfer）的方法。从实现的角度来看，通过利用共享表示和设计的目标，多个任务能以有效的方式相互学习。

  具体来说，在AdaMatting中，两个任务是trimap自适应和alpha估计。如上所述，trimap自适应可被建模为一个分割任务，将输入图像分割成前景、背景和半透明区域。结局此类分割问题的过程可能会产生丰富的语义特征，这反过来有利于解决alpha蒙板回归。

  我们采用了任务不确定损失（task uncertainty loss）而不是线性组合损失（linearly combined loss）。我们的损失可以表述为：

$$\mathcal{L}(\{\tilde{T}, \tilde{\alpha}\}, \{T_{opt}, \alpha_{gt}\}) = \frac{1}{2\sigma_1^2}\mathcal{L}_T(\tilde{T}, T_{opt}) + \frac{1}{\sigma_2}\mathcal{L}_\alpha(\{\tilde{T}, \tilde{\alpha}\}, \alpha_{gt}) + log2\sigma_1\sigma_2,\tag{3}$$

  其中$\tilde{T}$和$\tilde{\alpha}$代表trimap自适应和alpha估计的输出，$\sigma_1$和$\sigma_2$代表动态调整的任务权重，$\mathcal{L}_T$和$\mathcal{L}_\alpha$分别代表trimap自适应损失和alpha估计损失。更具体地，$\mathcal{L}_T$是交叉熵损失，$\mathcal{L}_\alpha$是$L_1$损失，仅在$\tilde{T}$（表示为$\tilde{T}_u$）的未知区域计算：

$$\mathcal{L}_\alpha(\{\tilde{T}, \tilde{\alpha}\}, \alpha_{gt}) = \frac{1}{|\tilde{T}_u|}\sum\limits_{s \in \tilde{T}_u}|\tilde{\alpha}(s) - \alpha_{gt}(s)|,\tag{4}$$

  其中$|\tilde{T}_u|$为$\tilde{T}_u$中的像素数。如3.1节所述，这种损失实际上将图像抠图分为了两部分，确保每个解码器分别学习结构语义和光度信息。

  注意，两个任务的折衷参数（trade-off parameter）在训练期间通过反向传播算法进行动态调整，从而避免了昂贵且繁琐的最优权重搜索过程。