A Style-Based Generator Architecture for Generative Adversarial Networks
原文链接
A Style-Based Generator Architecture for Generative Adversarial Networks. CVPR 2019: 4401-4410
摘要
借鉴了风格迁移(style transfer)文献,我们提出了一种生成对抗网络中生成器的替代结构。这种新的结构实现了自动学习的(automatically learned)、无监督的(unsupervised)高级属性(attributes)分离(例如,在人脸训练时的姿势和身份)和生成图像中的随机变量(stochastic variation)(例如,雀斑、头发),并且实现了直观的(intuitive)、可控的(scale-specific)的图像合成。新的生成器在传统的生成质量指标(distribution quality metrics)上达到了最高技术水平,可以显著提高插值特性(interpolation properties),并且可以更好地解构(disentangle)变量(variation)中的潜在因子(latent factors)。为了量化插值质量(interpolation quality)和解构(disentanglement),我们提出了两种新的自动化方法,适用于任何生成器结构。最后,我们介绍一个新的,非常多样性的并且高质量的人脸数据集。
2. 基于风格的生成器(Style-based generator)
传统上,潜在编码(latent code)通过一个输入层提供给生成器,例如,前馈网络(feedforward network)的第一层(Figure 1a)。我们从这个设计出发,省略了输入层,然后从一个已知的常量(learned constant)开始(Figure 1b, right)。在输入潜在空间(input latent space)$\mathcal{Z}$中给定一个潜在编码$\rm z$,一个非线性(non-linear)映射网络$f:\mathcal{Z} \rightarrow \mathcal{W}$会首先产生$\rm w \in \mathcal{W}$(Figure 1b, left)。为了简单起见,我们将两个空间的维度都设置为512,并且映射$f$使用8层MLP实现,我们将在4.1节中分析该决策。然后已知(learned)的仿射变换(affine transformation)将$\rm w$特化(specialize)为$\rm y = (y_s, y_b)$的风格,用于在合成网络(synthesis network)$g$的每个卷积层后面的适应性实例归一化(adaptive instance normalization, AdaIN)。AdaIN的操作被定义为
其中特征映射(feature map)$\rm x_ \it i$都是分别归一化的,然后使用来自风格$\rm y$的相应标量(scalar)进行缩放(scaled)和偏置(biased)。因此,每一层中的$\rm y$的维度都是feature map的两倍。
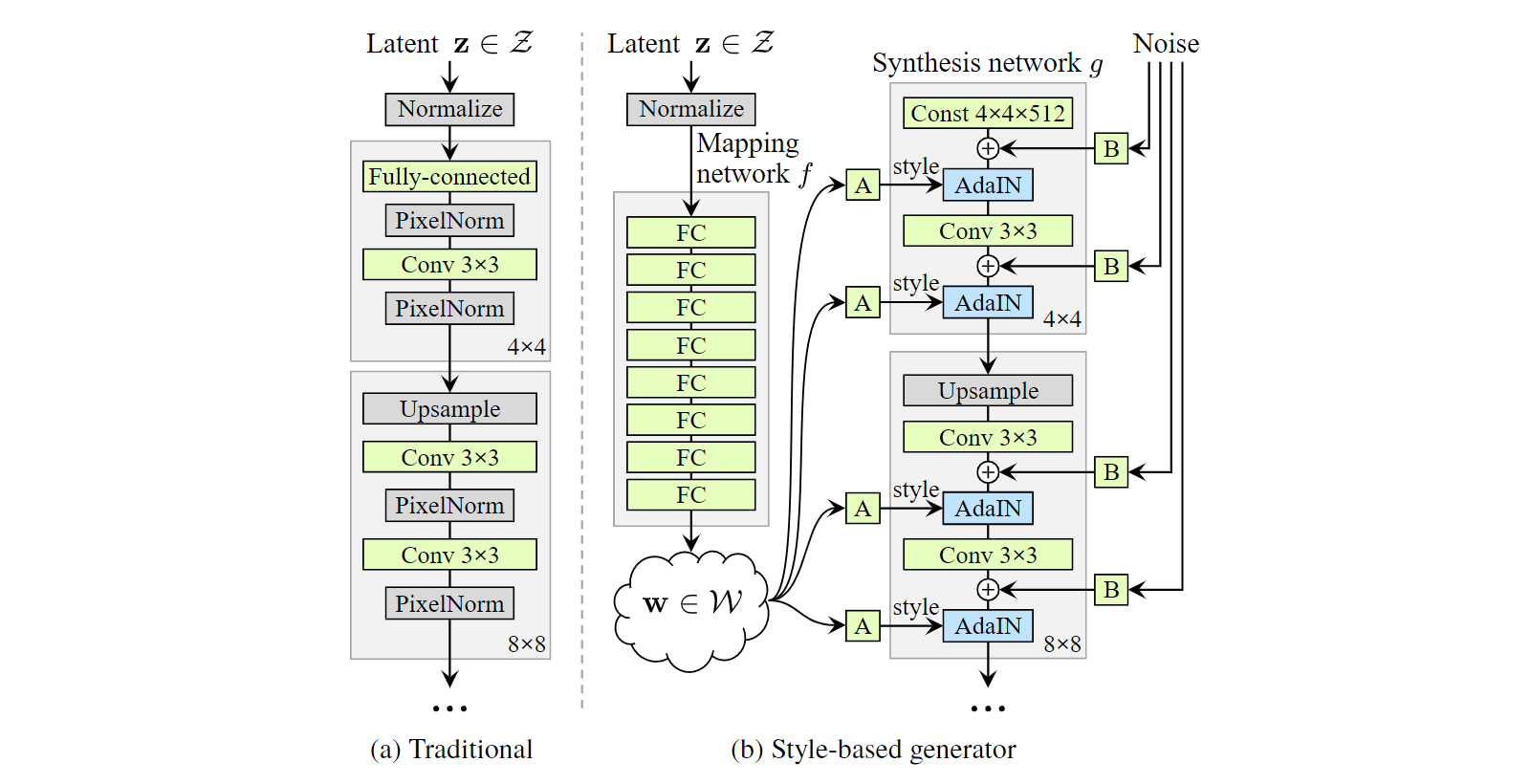
比较我们的方法和风格迁移,我们从向量$\rm w$而不是一张实例图像中计算出了空间不变(spatially invariant)的风格$\rm y$。我们选择重新使用“风格(style)”这个词来称呼$\rm y$是因为类似的网络结构已经用于了前馈风格迁移,无监督图像到图像(image-to-image)转换,和域混合(domain mixtures)。与一般的特征迁移(feature transforms)相比,AdaIN由于其高效性和紧凑的特征表示(compact representation),特别适合我们的目标。
最后,通过引入明确的(explicit)噪声输入(noise input),我们为生成器提供了一种生成随机细节的直接方法。这些是由不相关的高斯噪声组成的单通道图像,我们向合成网络的每一层提供一个专用的(dedicated)噪声图像。噪声图像使用特征比例因子(per-feature scaling factors)传播(broadcast)到所有feature map中,然后被添加到相应卷积的输出中,如Figure 1b所示。添加噪声输入的影响将在第3.2和3.3节中讨论。
2.1. 生成图像的质量
在我们研究生成器的特性之前,我们通过实验证明,新的设计不会影响图像质量,事实上,它大大提高了图像质量。Table 1给出了在CelebA-HQ数据集和我们的新的FFHQ数据集(Appendix A)上各个生成器结构的弗雷歇距离(Fréchet inception distance, FID)。补充资料中给出了其他数据集的结果。我们的基准配置(baseline configuration)(A)是Karras等人提出的Progressive GAN,除另有说明,我们借鉴了其网络及其所有超参数。我们首先通过使用双线性上/下采样操作,更长的训练时间和优化了的超参数,将其转换为改进了的基准(baseline)(B)。在补充资料中包含训练设置和超参数的详细说明。然后,我们通过添加映射网络(mapping network)和AdaIN操作(C)进一步改进了这一基准(baseline),并惊讶地发现,网络不再从向第一个卷积层输入潜在编码中受益。因此,我们通过移除传统的输入层并从一个已知的(learned)$4 \times 4 \times 512$常张量(constant tensor)(D)来开始图像合成。我们发现,尽管合成网络仅接收控制AdaIN操作的风格(styles),但合成网络依然能产生有意义的结果,这一点非常值得注意。
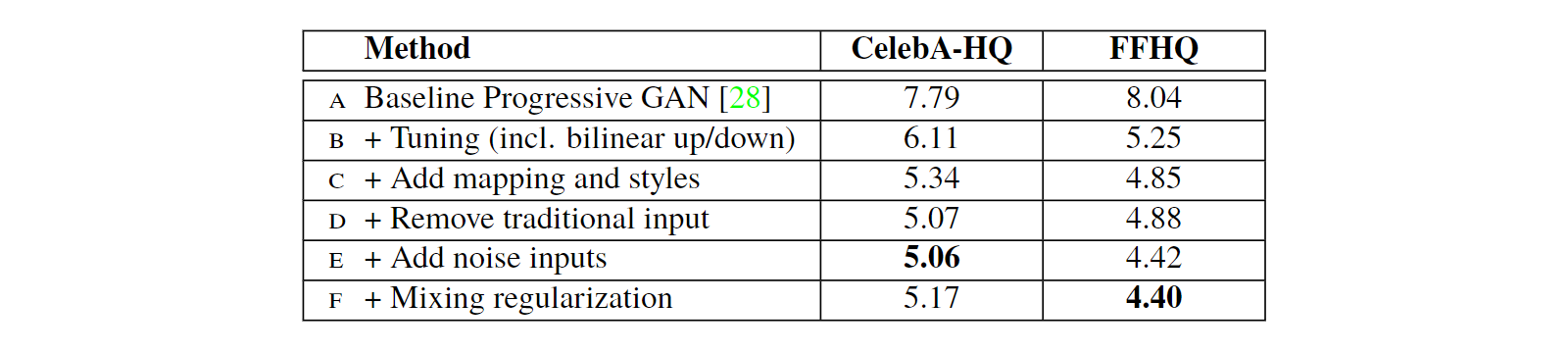
最后,我们介绍了进一步改善结果的噪声输入(noise input)(E),以及新的混合正则化(mixing regularization)(F),该正则化可以消除相邻风格的相关性,并对生成的图像进行更细粒度的控制(Section 3.1)。
我们使用两种不同的损失函数来评估我们的方法:对于CELEBA-HQ我们使用WGAN-GP,而FFHQ对配置A使用WGAN-GP,对配置B-F使用$R_1$正则化的非饱和损失函数(non-saturating loss)。我们发现这些选择可以得到最好的结果。我们的贡献不会修改损失函数。
我们观察到,与传统生成器(B)相比,基于风格的生成器(E)显著提高了FID,几乎提高了20%,证实了在并行工作中的大规模ImageNet测量。Figure 2展示了我们的生成器使用FFHQ数据集生成的一组未经处理的(uncurated)新图像。正如FID所证实的,平均质量很高,甚至眼睛和帽子等装饰也能成功生成。对于该图,我们使用了所谓的截断技巧(truncation trick)避免了从$\mathcal{W}$的极端区域取样——Appendix B详细说明了如何在$\mathcal{W}$而不是$\mathcal{Z}$中使用该技巧。注意我们的生成器只允许在低分辨率上选择性截断,这样高分辨率中的细节就不会受到影响。

本文中所有的FID都是在不使用截断技巧的情况下计算的,我们仅作为说明目在Figure 2和视频中使用了它。所有图像均以$1024^2$分辨率生成。
2.2. 先前的工作
大部分关于GAN结构的工作都集中在改进鉴别器上,例如,使用多个鉴别器,多分辨率(multiresolution)鉴别器或自注意力机制(self-attention)。生成器方面的工作主要集中在潜在空间的精确分布,或通过混合高斯模型,聚类或者促进凸性(encouraging convexity)来改造潜在空间。
最近的条件生成器将类标识(class identifier)通过一个单独的嵌入网络输入一个有大量层的生成器,而潜在标识(latent)仍然通过输入层提供。一些作者曾经考虑将部分潜在编码提供给多个生成器层。在并行工作中,Chen等人的“自我调节(self modulate)”生成器使用了AdaIN,类似于我们的工作,但不考虑中间潜在空间或噪声输入。
3. 基于风格的生成器的属性
我们的生成器结构可以通过指定比例修改风格来控制图像合成。我们可以将映射网络和仿射变换视为从已知分布(learned distribution)中为每个风格提取样本的一种方式,将生成网络视为基于一个风格集合(collection of styles)生成新图像的一种方式。每种风格产生的效果在网络中都是局部的(localized),即,修改风格的特定子集可能只影响图像的特定方面。
为了了解这种局部化的原因,让我们考虑AdaIN操作(Eq. 1)如何首先将每个通道归一化为零均值(zero mean)和单位方差(unit variation),并且仅基于风格来应用尺度(scale)和偏置(bias)。受风格的指示,新的每个通道的统计信息(per-channel statistic)修改了后续卷积操作特征的相对重要性,由于归一化,它们不依赖于原始统计信息。因此,在被下一个AdaIN操作覆盖之前,每个风格只控制一次卷积。
3.1. 风格混合
为了进一步促进风格局部化,我们使用了混合正则化,即在训练过程中使用两个随机潜在编码而不是一个生成指定百分比的图像。当生成这样的图像时,我们在生成网络中一个随机选择的点简单地从一个潜在编码切换到另一个潜在编码——一种我们称之为是风格混合的操作。具体来说,我们通过映射网络运行两个潜在编码$\rm z_1$,$\rm z_2$,并让相应的$\rm w_1$,$\rm w_2$控制风格,$\rm w_1$在切换点之前应用,$\rm w_2$在切换点之后应用。这种正则化技术可以防止网络假设相邻风格是关联的。
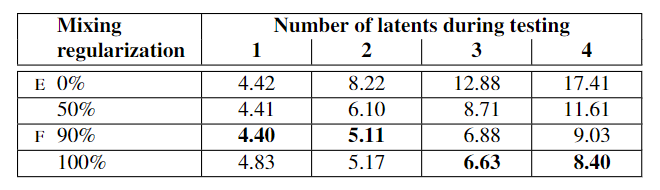
Table 2展示了训练过程中使用混合正则化是如何极大地提高局部化的,在测试中混合多个潜在标识的情况下,改进的FID表明了这一点。Figure 3展示了以不同比例混合两个潜在编码合成图像的示例。我们可以看到,风格的每个子集都控制着图像中有意义的高级属性。

3.2. 随机变化(Stochastic variation)
人像中有许多方面可以被视为是随机的,例如头发,胡茬,雀斑或皮肤毛孔的确切位置。只要它们遵循正确的分布,它们都可以随机化,而不影响我们对图像的感知。
让我们考虑一个传统的生成器是如何实现随机变化的。考虑到网络的唯一输入是通过输入层,网络需要发明一种方法,在需要时从前期激活函数中生成空间变化的伪随机数。这会消耗网络的容量,并且消除生成信号的周期性是很困难的——并且不总是成功的,生成图像中常见的重复模式(repetitive patterns)就证明了这一点。我们的网络结构通过在每次卷积之后添加像素级噪声的方式回避了这些问题。
Figure 4展示了我们使用不同噪声实现的生成器在同一基础图像上的随机效果。我们可以看到,噪声只影响随机层面,图片的整体构成和身份等高级层面完好无损。Figure 5进一步说明了将随机变化应用于不同层子集的效果。由于这些效果最容易在动画中展示,请参考随附的视频,在对比下了解改变一层的噪声输入如何导致随机变化。


我们发现有趣的是,噪声似乎紧紧地局部化(tightly localized)在了网络上。我们猜测在生成器的任一点上,都有尽快引入新内容的压力,而我们的网络产生随机变化最简单的方法就是依赖所提供的噪声。每一层都有一组新的噪声,因此没有激励(incentive)去生成前期的激活函数产生的随机影响,导致了局部效应。
3.3. 从随机性中分离全局影响(Separation of global effects from stochasticity)
前面的章节以及随附的视频表明,风格的改变会产生全局影响(改变姿势,身份等),噪音只会影响无关紧要的随机变化(不同方式梳理的头发,胡须等)。这一观察结果和风格迁移文献一致,在文献中已经确定,空间不变统计(spatially invariant statistics)(Gram矩阵,通道均值(channel-wise mean),方差等)可靠地编码了图像的风格,而空间变化特征(spatially varying features)编码了一个特定实例(a specific instance)。
在我们的基于风格的生成器中,风格会影响到整个图像,因为全部的feature map使用了相同的值进行缩放和偏置(scale and bias)。因此,姿势,光照和背景风格可以被连贯地控制。同时,噪声独立地添加到每个像素,因此非常适合控制随机变化。如果网络试图控制,例如,使用噪声控制姿势,这将导致空间不一致决策(spatially inconsistent decisions),将会受到判别器的惩罚。因此网络学会了在没有明确指导的情况下合理地使用全局和局部通道。
4. 解构学习(Disentanglement studies)
解构(disentanglement)有各种定义,但一个共同目标是一个由线性子空间(linear subspace)构成的潜在空间,每个子空间控制一个变化因子(factor of variation)。然而,$\mathcal{Z}$中的每个因子组合的抽样概率需要与训练数据中的概率密度相匹配。如Figure 6所示,这排除了与典型的数据集(typical datasets)和输入潜在分布(input latent distributions)完全分离的(disentangled)因子。
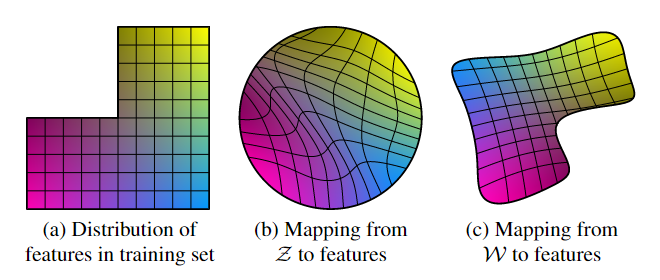
我们的生成器结构的一个主要优点是,中间潜在空间$\mathcal{W}$不必根据任何固定分布进行采样;其采样密度由已知的(learned)分段连续映射(piecewise continuous mapping)$f(\rm z)$导出。该映射可以用于“反翘曲(unwarp)”$\mathcal{W}$,从而使变化因子变得更加线性。我们假设生成器有这样做的压力,因为基于解构的表示(disentangled representation)比基于纠缠的表示(entangled representation)更容易生成真实的图像。因此,我们希望在无监督的环境中,即在变化因子事先未知的情况下,训练产生纠缠度较低的$\mathcal{W}$。
不幸的是,最近提出的量化解构的指标需要一个编码器网络(encoder network),将输入图像映射到潜在编码。这些指标不适合我们的目的,因为我们的baseline GAN缺少缺少这样一个编码器。虽然可以为此添加额外的网络,但我们希望避免将精力投入到实际解决方案之外的部分。为此,我们阐述了两种量化解构的新方法,这两种方法都不需要编码器或已知的变化因子,因此对于任何图像数据集和生成器都是可计算的(computable)。